投影与坐标系
❓︎❓︎❓︎
地球不是一个标准的球体，而是一个近似的椭球体，而我们常使用的地图是平面的，和球形毫无关系，那么地图是如何进行定位和展示的呢？
1. 地理坐标系
地球不是一个标准的球体，而是一个近似的椭球体，越靠近赤道则越宽。既然是一个三维物体，那么进行坐标系定位一般来说需要 x，y，z 一个三维坐标系来定义。 但是为了更好的在球面上进行定位，所以就采取了使用经纬度的方式。经线和纬线是地球表面上两组正交（相交为 90 度）的曲线，这两组正交的曲线构成的坐标， 称为地理坐标系地理坐标系（Geographic Coordinate System， 简称 GCS）。
1.1 WGS84
WGS84（World Geodetic System 1984）是全球定位系统（GPS）所使用的地理坐标系统和地球参考框架。它是由美国国防部开发的，广泛应用于导航、制图和地理信息系统（GIS）中。
- 椭球参数：
- 长半轴（a）：6378137.0米
- 扁率倒数（1/f）：298.257223563
- 短半轴（b）：6356752.3142米
- 原点：
- 原点位于地球质心（地球的重心），在赤道和本初子午线的交点处。
- 坐标系统：
- 经度（Longitude）：从本初子午线向东或向西测量，范围为-180°到+180°。
- 纬度（Latitude）：从赤道向北或向南测量，范围为-90°到+90°。
- 高程（Elevation or Height）：相对于椭球面的高度。
1.2 CGCS2000
CGCS2000（China Geodetic Coordinate System 2000）是中国大地坐标系2000，是中国国家测绘地理信息局（NGCC）建立的地理坐标系，广泛应用于国家测绘、地理信息系统（GIS）和导航等领域。
- 参考椭球参数：
- 长半轴（a）：6378137.0米
- 扁率倒数（1/f）：298.257222101
- 地心引力常数 GM＝3.986004418×1014m3s-2
- 自转角速度 ω＝7.292l15×10-5rad s-1
- 原点：
- 原点位于地球质心，参照国际大地参考框架（ITRF）。
- 坐标系统：
- 经度（Longitude）：从本初子午线向东或向西测量，范围为-180°到+180°。
- 纬度（Latitude）：从赤道向北或向南测量，范围为-90°到+90°。
- 高程（Elevation or Height）：相对于椭球面的高度。
2. 地图投影
地图投影就是指建立地球表面上的点与投影平面上点之间的一一对应关系。地图投影的基本问题就是利用一定的数学法则把地球表面上的经纬线网表示到平面上。在平时使用手机地图或者网页地图的时候，展现在我们面前的则是一个平面地图。如果说此时我们需要查询自己去某个饭店有多远，手机会告诉我们距离多少公里或者多少米，所以我们得到两个地点之间的距离是平面距离， 使用米或者千米为单位。而此时的定位坐标系，就被称作为投影坐标系（Projection Coordinate System，简称PCS）。
2.1 按照变形分类
地球表面是一个曲面，从曲面至平面的数学换算即为地图投影的过程，不同投影会引起不同类型的变形，例如，导致数据的形状、面积、距离或方向发生变形。
1）等角投影
等角投影保留局部形状。要保留描述空间关系的各个角，等角投影必须在地图上显示以 90 度角相交的垂直经纬网线。地图投影通过保持所有角不变来加以实现。缺点是由一些弧线围起来的区域将在此过程中发生巨大变形。地图投影无法保留较大区域的形状。
2）等积投影
保留所显示要素的面积。为此，形状、角和比例等其他属性将发生变形。在等积投影中，经线和纬线可能不垂直相交。有些情况下，尤其是较小区域的地图，形状不会明显变形，且很难区分等积投影和等角投影，除非加以说明或进行测量。
3）等距投影
保留某些点间的距离。任何投影都无法在整幅地图中正确保持比例不变。不过，多数情况下，地图上总会存在一条或多条这样的线：比例沿着这些线将正确地保持不变。多数等距投影都具有一条或多条这样的线：在此类线中，地图上线的长度（按地图比例尺计算）与地球上同一条线的长度相同，无论它是大圆还是小圆，是直线还是曲线。此类距离被视为真实距离。例如，在正弦投影中，赤道和所有纬线就是其真实长度。在其他等距投影中，赤道和所有经线具有真实长度。而其他投影（例如，两点等距离）仍会显示地图上一点或两点与相隔点间的真实比例。请记住，任何投影都不能实现地图上的所有点是等距离的。
2.2 按照投影方法分类
地图投影使用数学公式将地球上的球面坐标与平面坐标关联起来。
1）圆锥投影
最简单的圆锥投影是沿一条纬线与地球相切获得的投影。这条纬线称作标准纬线。所有的经线都投影到圆锥面上，并在圆锥的顶点或某一点处相交。纬线在圆锥面上的投影是一个个环。将圆锥沿任意一条经线“剪开”后即可获得最终的圆锥投影，投影中的经线显示为汇聚到一点的直线，而纬线显示为许多的同心圆弧。与剪开线相对的经线成为中央子午线。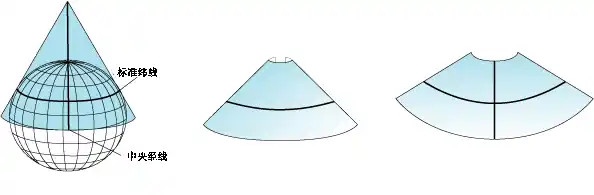 
较复杂的圆锥投影会与地球表面的两处位置相接触。这类投影被称作割投影，并带有两条标准纬线。也可以使用一条标准纬线和一个比例尺因子来定义割投影。在割投影中，标准纬线之间与标准纬线之外的部分变形模式是不同的。通常，割线投影的整体变形程度小于切线投影。在更复杂的圆锥投影中，圆锥的轴并不与地球的极轴重合。此类投影称作斜轴投影。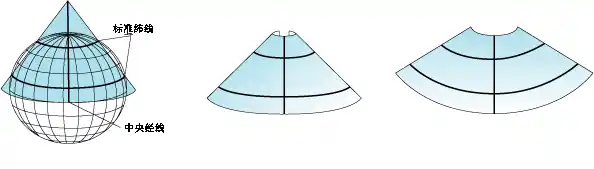 
2）圆柱投影
与圆锥投影类似，圆柱投影也存在相切或相割两种情况。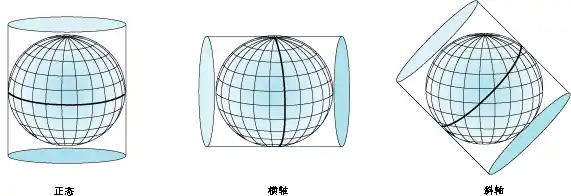 
墨卡托投影是最常用的圆柱投影之一，并且通常以赤道为切线。经线以几何方式投影到圆柱面上，而纬线以数学方式进行投影。这种投影方式产生成 90 度的经纬网格。将圆柱沿任意一条经线“剪开”可以获得最终的圆柱投影。经线等间距排列，而纬线间的间距越靠近极点越大。此投影是等角投影，并沿直线显示真实的方向。在墨卡托投影中，恒向线、等方位角线是直线，但大多数的大圆都不是直线。
对于更复杂的圆柱投影，圆柱发生了旋转，因此切线和割线的位置发生了变化。横轴圆柱投影，例如横轴墨卡托投影，使用经线作为相切的接触线，或使用平行于经线的线作为割线。这样标准线即为南北方向的线，且其上的比例是真实的。斜轴圆柱是围绕赤道和经线间的任意大圆线旋转而成的圆柱。在此类更加复杂的投影中，大多数经线和纬线都不再是直线。
3）平面投影
平面投影将地图数据投影到与地球接触的平面。平面投影也称为方位投影或天顶投影。 
此类型的投影通常在一点与地球相切，但也可能相割。接触点可以是北极、南极、赤道上的某点或者赤道与两极之间的任意点。此点会指定投影中心，并将作为投影的焦点。焦点由中央经度和中央纬度标识。可能的投影方法包括极方位投影、赤道投影和斜轴投影。
极方位投影是最简单的形式。纬线是以极点为中心的同心圆，经线是在极点处与其真实的方向角相交的直线。在其他投影方法中，平面投影在焦点处将具有 90 度的经纬网格角度。由焦点确定的方向是精确的。
穿过焦点的大圆由直线表示；因此从中心到地图上其他任意点的最短距离是直线。面积和形状变形后的图案是以焦点为中心的圆。由于这个原因，方位投影更适合圆形区域，而不太适合矩形区域。平面投影最常用于绘制两极地区的地图。
某些平面投影会在空间中从特定点来观测表面数据。观测点将确定球面数据如何投影到平面。在不同的方位投影中，用于观测所有位置的透视图也有所不同。透视点可以是地球的中心、与焦点正对的表面点或者地球外部的某点，就如同从卫星或其他星球上遥看一样。
有部分方位投影是按焦点和透视点（如果适用）分类的。球心投影从地心来观测表面数据，而立体投影是在两极之间进行观测。正射投影从无穷远点（如同从外太空）观察地球。注意观察透视图之间的差异如何决定与赤道相对的变形程度。
3. 墨卡托投影
墨卡托投影是最常用的圆柱投影之一，并且通常以赤道为切线。
1）墨卡托投影
墨卡托投影 （Mercator Projection）是在1569年，当时的地理学家杰拉杜斯·墨卡托提出的一种角度不变的投影方式，又被称作为等角正切圆柱投影。我们可以想象一下，将地球置于一个空心圆柱体中，其中地球的赤道正切于圆柱体。然后假设地心有一个灯泡，灯泡的光线能够透过地表照射到圆柱体表面，那么地球球面上的绝大部分区域都会相应的被投影到圆柱体上。此时将圆柱体展开，以赤道的投影为横坐标，以本初子午线的投影的纵坐标，就得到了以墨卡托投影所构成的平面坐标系。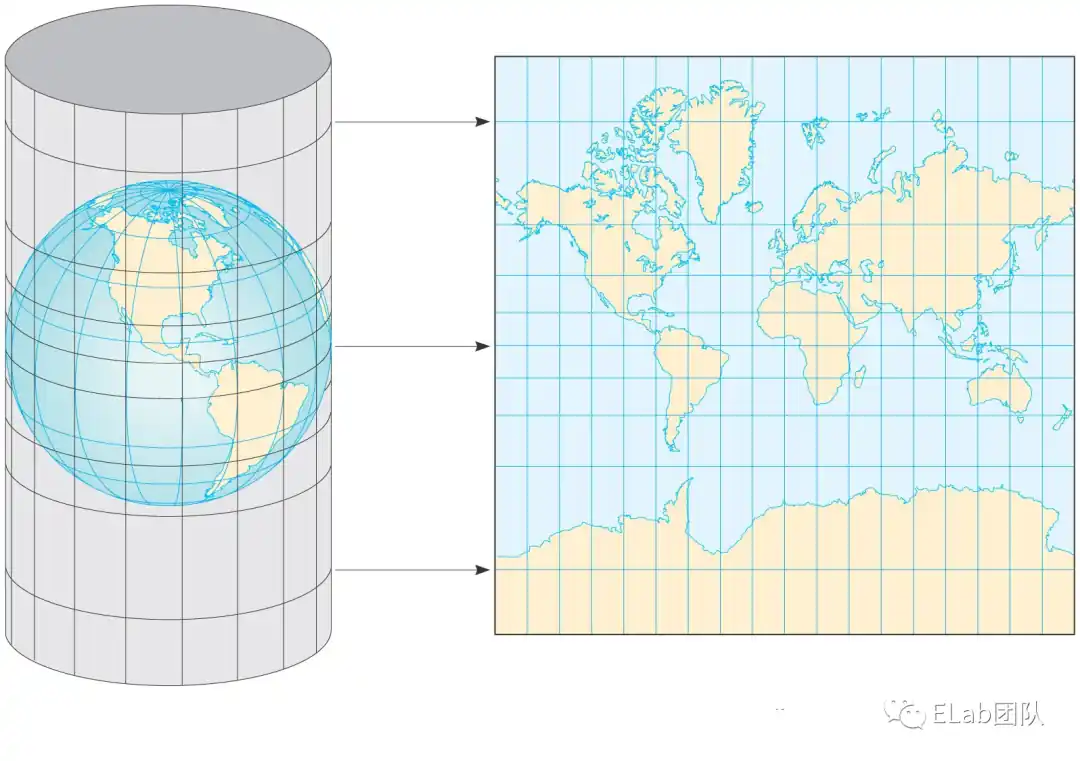 
我们可以看到该投影有以下特点：
- 经线、纬线分别为平行直线，并且经纬线之间互相垂直
- 纬度越高的地方，投影面积形变越大，而在纬度无限接近于极点的位置，面积则会无限大，因此纬度的上限和下限分别是北纬 89° 和南纬 89°。
- 虽然在面积上有形变，但是是各个方向上的均等扩大，所以保证了地图方向、角度以及位置关系的正确性。
2）Web墨卡托
web墨卡托，也称伪墨卡托（Pseudo Mercator Projection） ，属于一种不严格的墨卡托投影方式，其被 Google Map 最先发明，后续又被Bing，百度， OSM 等各个网络地图服务商使用，因此成为了互联网电子地图最常见的投影方式。
其和墨卡托投影的最大区别在于，墨卡托投影是建立在地球是一个椭球体的基础上进行投影公式计算的，而 Web 墨卡托在其计算公式上直接将椭球体变成了球体，大大简化了投影转化的计算方法。 
其中 x, y 为投影坐标系中的坐标值，α为赤道半径，θ为经度，ψ为纬度。
此外，web 墨卡托投影一般默认为一个正方形。已知赤道半径为 6378137 米，则赤道的周长则为 约为40075016.68557849，所以投影坐标系中 X 轴的范围为 [-20037508.342789244, 20037508.342789244]，则 Y 轴的范围也为 [-20037508.342789244, 20037508.342789244]，可以通过上面公式反算出纬度被限制在了[-85.0511287， 85.0511287] 范围内。
4. EPSG
前面提到了地理坐标系和投影坐标系，还提到了一些投影方法。就拿墨卡托和web墨卡托来说，前者是将地球看作一个椭球体，后者将地球看作了一个球体。所以说我们并没有一个严格的标准且统一的方式来表述某个点的位置。当没有统一标准的时候，就会存在很多体系标准，而当各种体系标准变得庞大且失去统一管理的时候，人们想将不同体系之间的坐标互相转化的话就会变得异常困难。EPSG 就是来管理这些坐标体系的一个组织。
EPSG通过WKID 来管理不同的坐标体系，WKID简单理解就是 ID，每个坐标体系拥有独一无二的ID。
4.1 大地坐标系
大地坐标系是以参考椭球面为基准面而建立起来的坐标系，也可以简单理解成属于地理坐标系的一种。大地坐标系又分为参心大地坐标系和地心大地坐标系。其中参心坐标系是以椭球几何中心为原点构建的坐标系，一般用来对局部地区大地测绘使用，而地心坐标系是以地球质心为原点构建的坐标系，一般用来对地球整体大地测绘使用。
4.2 WGS84（EPSG:4326）
WGS84则属于地心大地坐标系，是世界上第一个统一的大地坐标系，所以也被称为世界大地坐标系，而我们常说的GPS定位系统就是依据此坐标系建立的。除了中国地区以外，很多电子地图比如谷歌、Bing等都是用的是 WGS84。
4.3 CGCS2000（EPSG:4490）
我国在上世纪50年代和80年代分别建立了北京54和西安80参心大地坐标系，后随着社会经济，科学的发展，中国测绘、地震部门和科学院有关单位重新建立了中国新一代地心大地坐标系，也就是CGCS2000，所以也被称为2000国家大地坐标系。
和WGS84相比，两者本质上可以算是一致的，只是在计算过程中采用的参数有细微的差别。
4.4 Web墨卡托（EPSG:3857)
其实原本 EPSG 不准备将 web 墨卡托纳入 WKID，因为 web 墨卡托毕竟是采用了不严谨的假设，使得原本是等角投影的墨卡托变成了近似等角，从而直接影响到投影坐标的精度。但是随着 web 墨卡托在 web 领域被广泛使用从而名声大噪，EPSG 也只能将其接受。
5. GCJ02 和 BD09
5.1 GCJ02
GCJ02 是中国国家测绘局所制定的坐标系统，其本质就是在 WGS84 经纬度的基础上进行了一层加密。由于国家相关安全保密规定，我国所有对外的地图系统都需要进行加密。所以高德以及谷歌的中国地图都是使用GCJ02坐标系。所以如果在 GCJ02 的坐标系下直接使用 GPS 的经纬度坐标，那么就会得到一个错误的定位地点。所以 GCJ02 坐标系在业内也常常被称为火星坐标系。
在手机上下载一个GPS定位软件（部分硬件设备获取的GPS信息是原始的GPS信息，而一般地图软件的定位信息都是GCJ02加密过后的），得到天安门的经纬度是 39.907375,116.391349。 
5.2 BD09
百度在GCJ02 的基础上又进行了一层加密，这就是 BD09。